Топологические особенности плотности состояний и свойства твердых тел

© П.А. Игошев, В.Ю. Ирхин

Топологические особенности плотности состояний и свойства твердых тел

П.А. Игошев, В.Ю. Ирхин

Как известно из элементарного курса физики, динамические свойства свободной частицы, находящейся в однородном пространстве, вполне характеризуются ее массой m, так что  зависимость ее энергии от импульса p имеет вид ε(p) = p²/2m. Однако при помещении частицы в окружение кристаллической решетки  твердого тела ее поведение может кардинально меняться. Именно это  обстоятельство делает столь привычный нам объект, как твердое тело, вместилищем крайне необычных и разнообразных эффектов – сильный магнетизм, сверхпроводимость, локализация мобильных электронов (формирование магнитных моментов), состояние с  тяжелыми фермионами и многое другое, – все они описываются и объясняются квантовой механикой, где привычная интуиция макромира перестает работать. Согласно теореме Блоха, см. [1], спектр любой частицы ε(k) в периодическом окружении обладает свойством периодичности по  квазиимпульсу k – обобщению импульса на пространственно неоднородные (но периодические) системы.

Таким образом, главным эффектом кристаллической решетки является сворачивание неограниченного «пространства импульсов» однородной системы в бесконечное (счетное) число копий ограниченной области этого пространства (более строго, обратного пространства), которая называется зоной Бриллюэна (каждая копия производит ветку спектра — зону). Геометрически зона Бриллюэна представляет собой многогранник в обратном пространстве, имеющий ту же симметрию, что и кристалл твердого тела.

Аналогия квазиимпульса k и обычного импульса p проявляется в том, что электрон может сохранять в кристаллической решетке свой квазиимпульс бесконечно долгое время – аналогично тому, как свободная  частица движется равномерно и прямолинейно, сохраняя свой импульс. Следующим следствием ограниченности зоны Бриллюэна является ограниченность спектра ε(k) частиц как функции квазиимпульса и, следовательно, наличие его минимумов (имеется ровно один для обычной частицы) и максимумов (не может быть для обычной частицы), а также седловых точек – значений квазиимпульса, где кривизна функции ε(k) меняет свой знак.

Обязательное существование k-точек всех этих типов для любого твердого тела имеет топологическую природу и поэтому защищено от таких воздействий, как деформация (изменение параметров решетки и ее точечной симметрии), и внутренних взаимодействий (электрон-электронное, электрон-фононное и т.п.), которые часто важны  в реальных кристаллах. Об этом говорит  теорема Ван Хова [2], которая утверждает обязательное существование седловых точек спектра для любой решетки, что особенно важно для электронных свойств твердого тела. В дальнейшем мы постараемся забыть о движении электрона в обычном (как говорят физики, прямом) пространства, то есть «прямой» решетке, и будем относить понятия точек, линий и т.д. исключительно к зоне Бриллюэна обратного пространства.

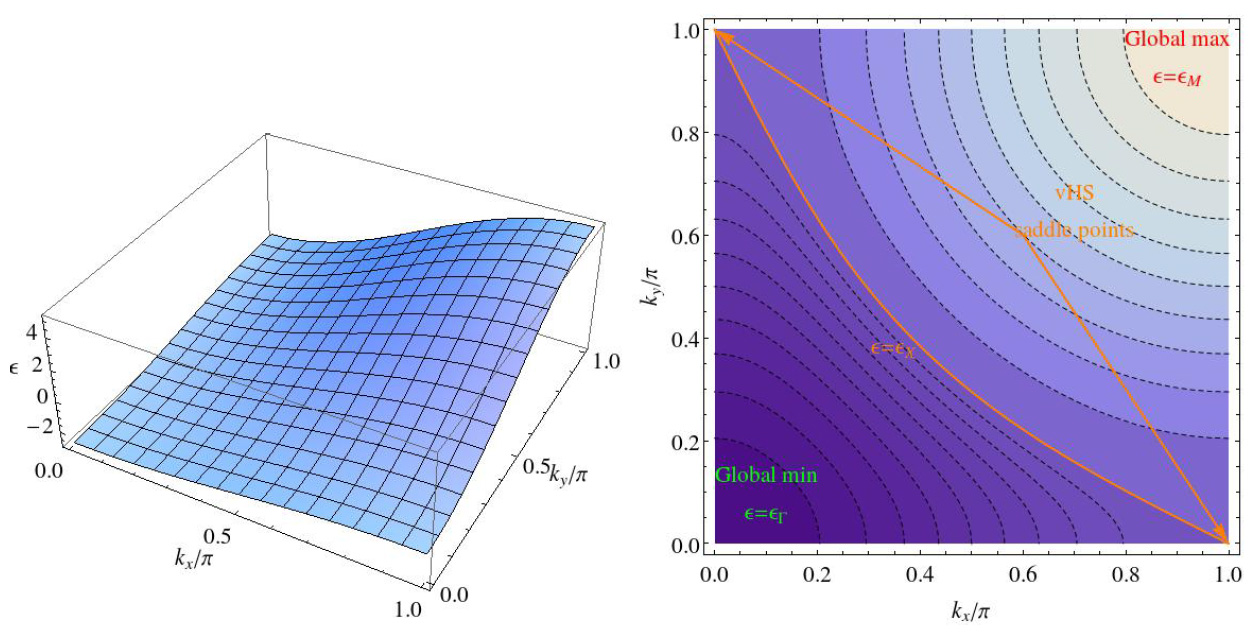
Рис. 1. a) Спектр ε(k) как функция квазиимпульса в первом квадранте зоне Бриллюэна при отношении интегралов переноса τ = 0.3. b) То же на контурном графике, где линиями показаны изоэнергетические контуры.

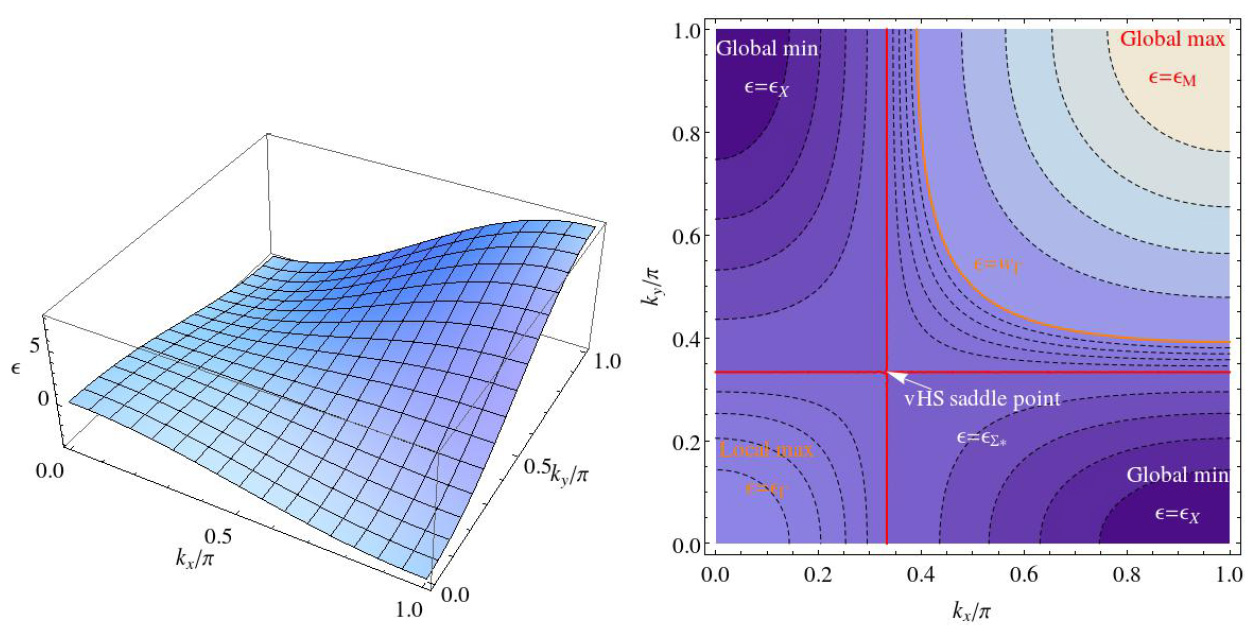
Рис. 2. То же, что и на рис. 1 при τ = 1.0.

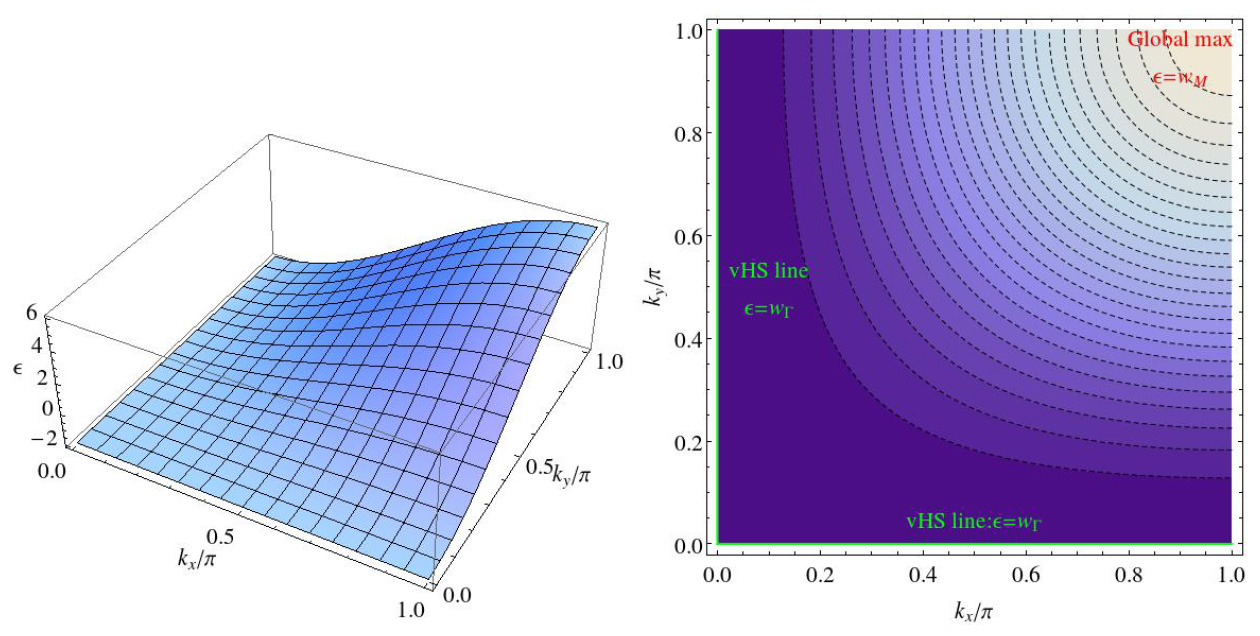
Рис. 3. То же, что и на рис. 1 при τ = 0.5.

Современные вычислительные методы позволяют рассчитать спектры элементарных возбуждений (электронов и фононов – квантов колебаний решетки) как функции k для любых соединений в некоторых приближениях. (Качество таких приближений является разным для разных соединений и является центральным вопросом физики сильнокоррелированных систем). Однако значимые детали, обусловленные и «защищенные» топологией, часто оказываются настолько деликатны, что не могут быть напрямую оценены из этих вычислений и требуют особого исследования.

Термодинамические свойства твердых тел при низких температурах определяются группой занятых электронных состояний, которые образуют «море Ферми» – анизотропное обобщение сферы Ферми, известной из теории квантовых газов. Чем слабее меняется электронный спектр в зависимости от k, тем больше электронов находится в группе состояний с примерно равным значением энергии на границе моря Ферми. Соответствующий уровень электронной энергии называется энергией Ферми E_F, причем именно электроны, имеющие энергию, близкую к E_F, подвержены температурному возбуждению.

В случае, когда емкость ρ(ε) этой группы (то есть плотность электронных состояний с энергией ε) велика, реализуются различные неустойчивости электронного состояния твердого тела, проявляющиеся как фазовые переходы, а также необычные температурные зависимости электронной теплоемкости и других свойств твердого тела.

При модельных исследованиях электронных свойств твердых тел в большинстве случаев достаточно ограничиться учетом энергии перескоков электронов (вызванных полем соседних узлов решетки и определяющих энергетический спектр) лишь между ближайшими и следующими за ближайшими узлами решетки. Таким образом, единственным существенным параметром оказывается отношение второго и первого интеграла переноса τ.

Важное значение имеют изоэнергетические поверхности – множества точек, энергия которых имеет одну и ту же величину ε. Можно показать, что ρ(ε) равно среднему «времени» движения по «орбите», получаемой сечением изоэнергетической поверхности, если считать, что скорость движения по орбите совпадает с градиентом спектра ∂ε(k)/∂k, то есть с групповой скоростью. На этом языке энергии вблизи минимума и максимума спектра производят орбиты, подобные эллиптическим кеплеровским, а седловые точки соответствуют гиперболическим траекториям кеплеровой задачи, т.е. идущим из бесконечности и уходящим в бесконечность. Однако, в отличие от задачи Кеплера, где тип траектории определялся лишь знаком полной энергии, здесь ситуация является более сложной. Примеры орбит для двумерной задачи можно увидеть ниже на рис. 1–3 (изоэнергетическая поверхность в двумерном случае сводится к орбите).

Существует общая связь особенностей функции ρ(ε) и топологических свойств спектра ε(k) [2]. Если скорость возбуждений v(k) = ∂ε(k)/∂k обращается в нуль в точке k, то такая точка называется точкой ван Хова. Уровни энергии ε = ε(k), соответствующие точкам ван Хова, и только они соответствуют особенностям ρ(ε) как функции ε. Наиболее сильные особенности соответствуют седловой k-точке, в которой нет ни максимума, ни минимума спектра, а профиль графика ε(k) напоминает седло.

Взаимосвязь топологических свойств спектра (рис. 1–3) и поведения ρ(ε) (рис. 4) наиболее просто увидеть на модельном примере двумерной квадратной решетки. При τ = 0.3 (рис. 1) имеется минимум ε(k) при k = (0,0), максимум – при k = (π,π) и две седловых точки k = (0,π), (π,0), где кривизна спектра меняет свой знак (это хорошо видно на графике изоэнергетических поверхностей). При τ = 1.0 (рис. 2) имеется локальный максимум ε(k) при k = (0,0), минимумы – при k = (0,π), (π,0) и седловые точки на диагоналях. Интересно, что положение седловой точки на диагонали дрейфует с изменением τ > 1/2: чем больше τ отклоняется от 1/2, тем дальше смещается от k = (0,0). Глобальный максимум при k = (π,π) сохраняется. Таким образом, при увеличении τ происходит топологический переход. Точка ван Хова k = (0,0) меняет свой тип (минимум заменяется на максимум), k = (0,π) меняет тип с седловой на минимум. Это происходит при τ = τ_* = 1/2, когда уровни энергии этих точек сливаются и формируются целые линии таких точек ван Хова (k_x= 0 и k_y = 0), имеющие одинаковую энергию (рис. 3). В окрестности этих точек спектр является наиболее плоским. Таким образом, линия ван Хова, имеющиеся при τ = 1/2, распадаются на три точки: седловая точка на диагонали, точка локального максимума k = (0,0), производящая скачок, и точка k = (0,π) (и эквивалентная ей k = (π, 0)).

Из рис. 4 видно, что точка логарифмического обращения ρ(ε) в бесконечность смещается при изменении τ, но всегда сохраняется в силу своей топологической защищенности: по теореме ван Хова [2] седловая точка присутствует всегда в спектре двумерной системы и производит логарифмическую расходимость ρ(ε) при некотором значении энергии ε = ε_VH. В точке топологического перехода, при τ = 1/2, логарифмическая особенность заменяется более сильной, корневой, происходящей от линий ван Хова и слабой k-зависимости спектра в окрестности этих линий. При τ > 1/2 имеется скачок ρ(ε), поскольку ее значение становится вдвое меньше, когда энергия становится выше энергии локального максимума при k = (0,0).

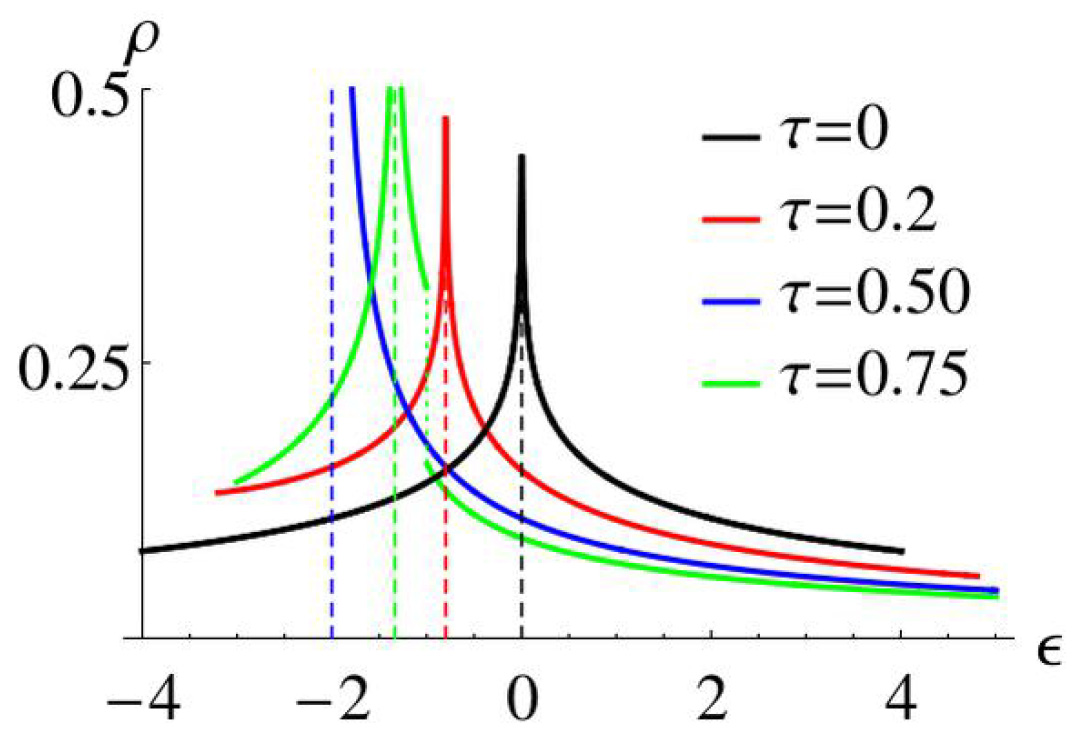
Рис. 4. Плотность состояний ρ(ε) как функция энергии ε для квадратной решетки при различных значениях τ. Пунктирной линией показан уровень энергии, соответствующий энергии седловых точек и сингулярностям ван Хова ρ(ε). Коротким пунктиром показан скачок ρ(ε) при τ = 0.75. Здесь и ниже в качестве единицы измерения энергии выбирается энергия (интеграл) переноса между ближайшими соседями.

Для трехмерных (кубических) решеток (всегда существующие) седловые точки ван Хова в одиночку не могут привести к обращению ρ(ε) в бесконечность. Однако если такие k-точки формируют линию [3], это может привести к расходимости плотности состояний, причем она совпадает с точкой топологического перехода в электронном спектре. Это проявляется и в том, что точка фокуса части изоэнергетических орбит меняется. Отклонение параметров от этого случая приводит к распаду линии ван Хова на несколько точек ван Хова (две-три), когда ρ(ε) в какой-то мере сохраняет особенности (большая величина и резкая зависимость).

Мы получили точные формулы для ρ(ε) через эллиптические интегралы [4,5] и построили графики при различных значений τ для примитивной кубической (ПК) и объемноцентрированной (ОЦК) решеток; результаты расчета показаны на рис. 5. Для ПК решетки линия ван Хова возникают при τ = 1/4, что приводит к расходимости типа обратного корня четвертой степени. Если τ > 1/4, эта линия распадается на несколько точек, формирующих симметричное плато (пример – τ = 0.4 на рис. 5a). Это плато является устойчивой особенностью, защищенной топологически. Для ОЦК решетки линии ван Хова имеются при τ = 0 (логарифмического типа) и τ = 1 (типа обратного корня четвертой степени). При отклонении τ от этих значений линии ван Хова распадаются на несколько точек, формирующих асимметричное плато (пример – при τ = 1.1) с резким падением ρ(ε).

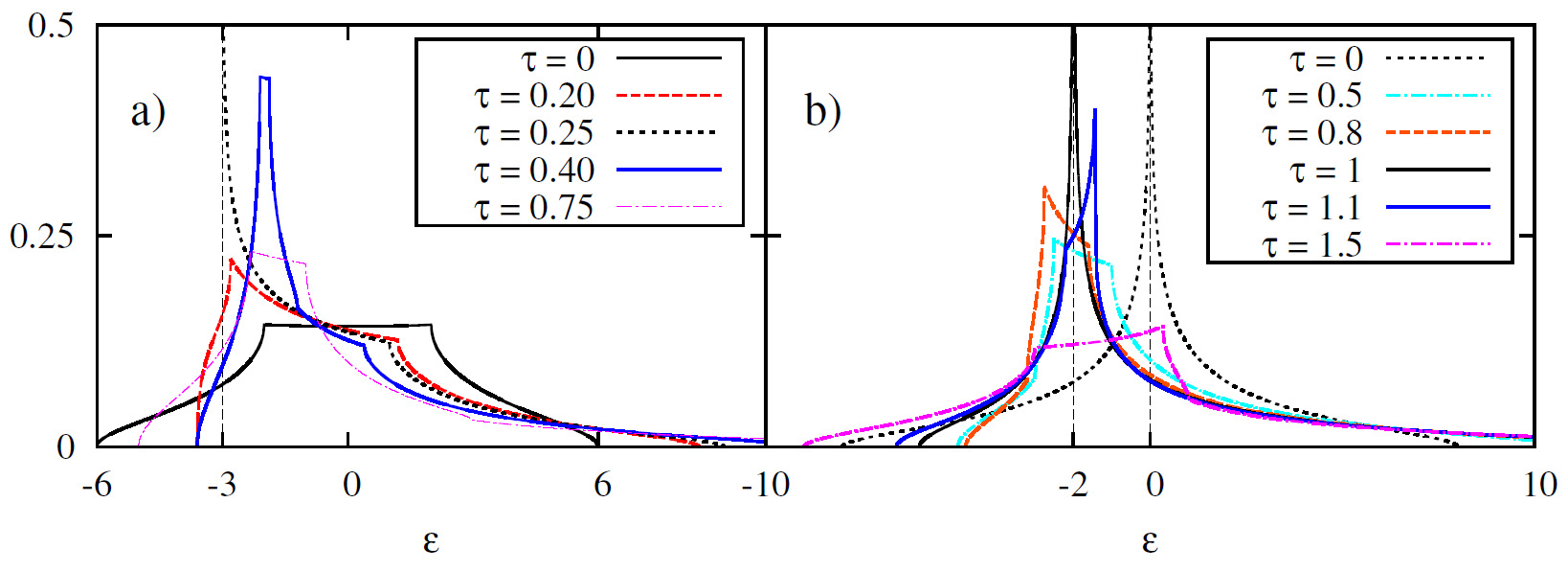
Рис. 5. ρ(ε) для ПК (a) и ОЦК (b) решетки при различных τ. Вертикальным пунктиром показано положение гигантских сингулярностей ван Хова.

С другой стороны, если спектр, полученный в рамках расчетов, является слабодисперсионным на некотором участке в каком-то направлении зоны Бриллюэна, то в окрестности этого участка имеется точка с большой массой или пара таких точек, появляющихся в результате распада линии.

Для иллюстрации влияния особенностей на электронные свойства на рис. 6 и 7 приведены результаты расчета электронной теплоемкости С для ПК и ОЦК решеток при низких температурах, наряду с графикам сингулярной плотности состояний на соответствующем масштабе энергий. Были выбраны значения τ, близкие к соответствующим топологическим переходам, и уровень Ферми E_F, находящийся внутри структуры ван Хова, которая остается от распада линии ван Хова: для ПК решетки линия ван Хова, имеющаяся при τ = 0.25 распадается при τ > 0.25 на три точки Λ^*, Σ^* и Г, в окрестности которых спектр слабо меняется; для ОЦК решетки линия ван Хова, имеющаяся при τ = 1.0, распадается на точки Δ^*, Г и N при τ > 1.0. Для наглядности приведен также расчет для E_F = 0, удаленного от всех особенностей. В этом случае электронная теплоемкость линейно зависит от температуры.

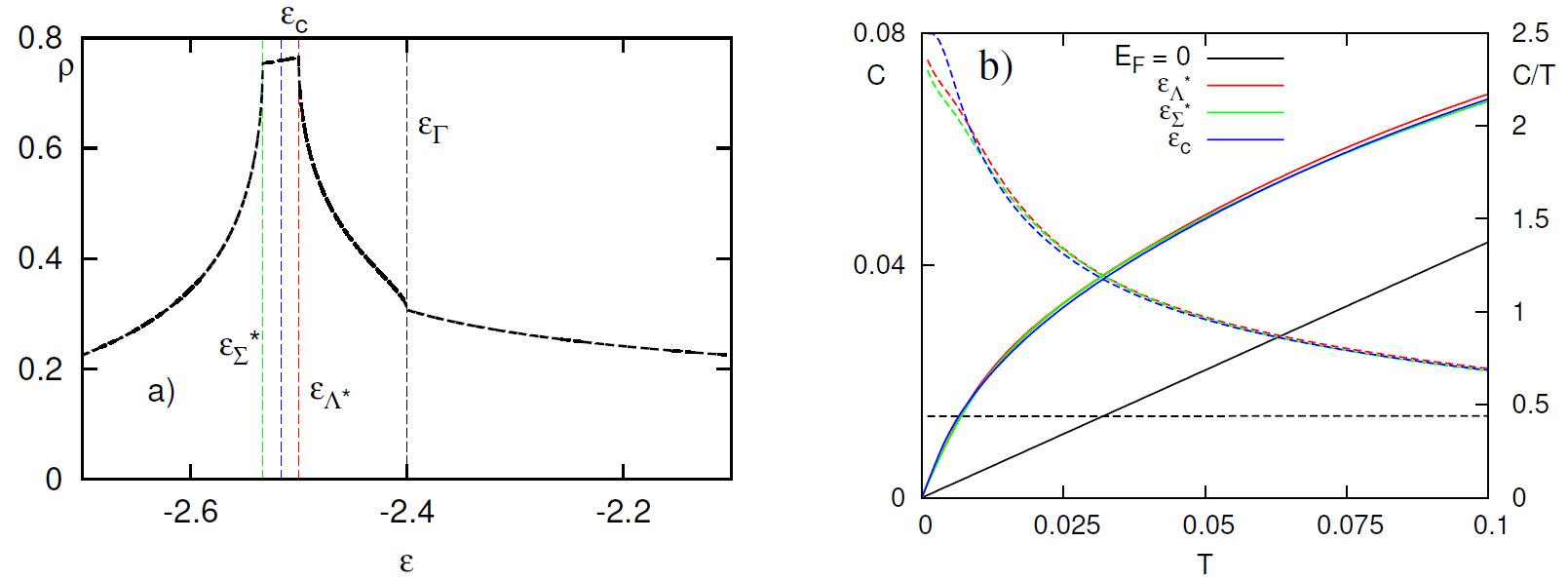
Рис. 6. a) График плотности состояний при τ = 0.3 для ПК решетки в окрестности нескольких уровней ван Хова («плато ван Хова»). Вертикальными линиями показаны значения энергии на краях пика, соответствующих энергиям ван Хова ε_Λ* и ε_Σ*, и в центре пика ε_c, которым соответствует выбор уровня Ферми на рис. 6b). b) Температурная зависимость теплоемкости C (левая ось, сплошные линии) и коэффициента γ = C/T (правая ось, пунктир) при различных положениях уровня Ферми, выбранных при разных энергиях на плато ван Хова (цвета вертикальных линий рис. a) соответствуют цветам кривых рис. b). Для сравнения приведет случай E_F = 0, когда нет влияния особенностей ван Хова.

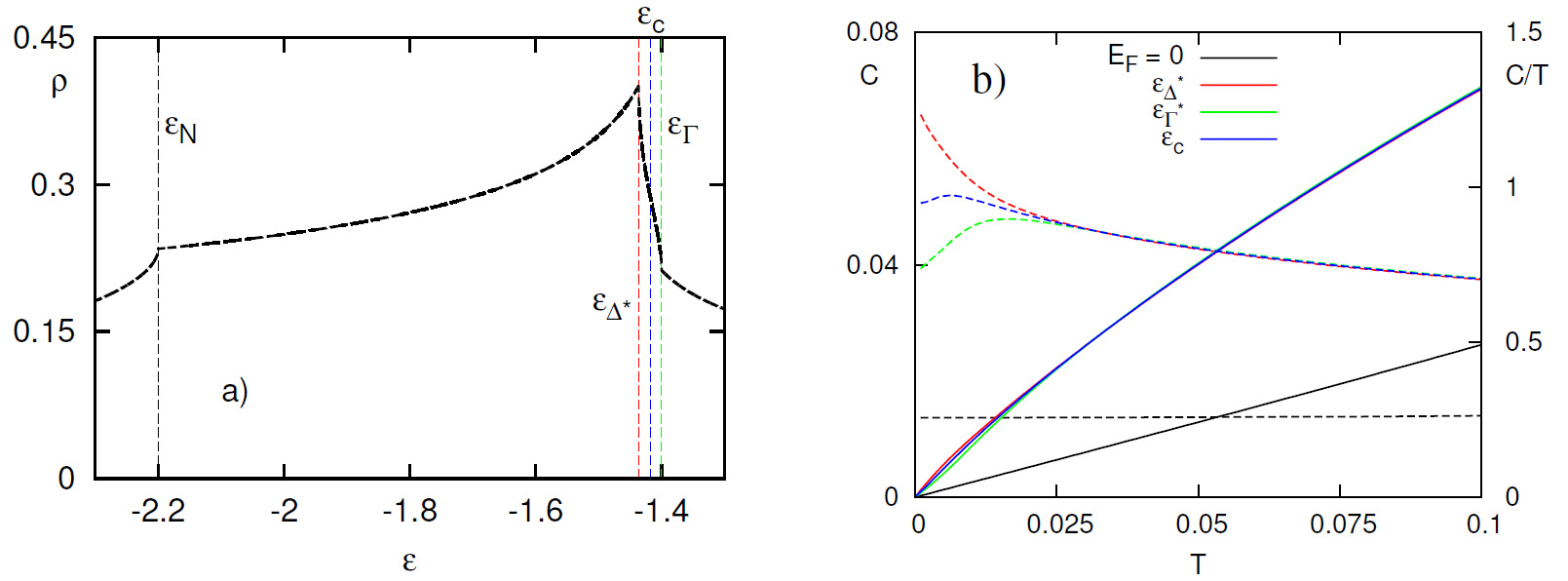
Рис. 7. То же, что и на рис. 6, при τ = 1.1 для ОЦК решетки. Показаны уровни энергии ван Хова ε_Δ*, ε_Г и ε_N.

Видно, что теплоемкость для ПК и ОЦК решеток увеличена и очень сильно отклоняется от стандартной линейной температурной зависимости, причем это поведение сохраняется далеко за пределами температурного масштаба порядка ширины пика T_* ≈ 0.03. Имеется также существенная зависимость от положения уровня Ферми в пределах структуры ван Хова при T << T_*.

Литература

1. С.В. Вонсовский, М.И. Кацнельсон. Квантовая физика твердого тела. - М.: Наука. Главная редакция физико-математической литературы (1983).
2. L. Van Hove, Phys. Rev. 89, 1189 (1953).
3. С.В. Вонсовский, М.И. Кацнельсон, А.В. Трефилов, Физика металлов и металловедение 76(3), 3 (1993).
4. P.A. Igoshev, V.Yu. Irkhin, Physics of Metals and Metallography 120, 13, 1282 (2019).
5. П.А. Игошев, В.Ю. Ирхин, Письма в ЖЭТФ 110, 11, 741 (2019).

Краткая формула